强化学习中的A3C算法

2017-12-17

1. A3C(Asynchronous Advantage Actor Critic)算法背景介绍

A3C算法[1]由DeepMind在2015年提出，基于Actor-Critic框架(参考下文)，并且通过异步并行训练多个agent的方式，在Atari 2600、TORCS、MuJoCo等视频游戏中都取得了优异的效果。此外，A3C既能适应于离散动作空间的控制，也能适应于连续动作空间的控制。

2. Actor-Critic(行动家-评论家)算法介绍

结合使用强化学习中经典的值函数方法和策略梯度方法，所谓的Actor即是策略输出函数，根据agent的状态state产生输出动作action，直观上可以认为它作为大脑来控制agent的行动；Critic即为每个状态的值函数，根据训练过程中获得的历史回报reward来自我调整，同时影响Actor的训练。
论文中的Actor和Critic都使用卷积神经网络来近似，两者共享相同的卷积层，但对应于不同的输出。

2.1 策略网络

$\pi(a|s, \theta)$即为策略函数，根据状态s直接输出动作a，$\theta$是需要优化的参数，优化目标是使得好的策略的出现概率高，坏的策略的出现概率低。
根据策略梯度定理，可以得到$\theta$的更新公式为：$\theta \leftarrow \theta + (\sum\limits_{t=1}^{T}\triangledown_{\theta}log\pi(a_{t}|s_{t}; \theta))(\sum\limits_{t=1}^{T}r(s_{t}, a_{t}))$，但直接这样做带来的问题是高方差、学习效率低，因为这里的梯度值对于所有action来说都是正的。
在Actor-Critic框架中，引入了基于状态值函数估计得到的Advantage函数$A^{\pi}(s,a)=r(s,a)+\gamma V^{\pi}(s’) - V^{\pi}(s)$来辅助更新策略函数的参数，这里使用值函数作为一种baseline，降低了实际更新时参数的方差，advantage函数可看作在状态s采取行动a时，相对于当前状态值函数的一种优势。因为值函数是对状态未来预期价值的一种估计。于是，这里$\theta$的更新公式变成$\theta \leftarrow \theta + (\sum\limits_{t=1}^{T}\triangledown_{\theta}log\pi(a_{t}|s_{t}; \theta))(\sum\limits_{t=1}^{T}(r(s_{t},a_{t})+\gamma V^{\pi}(s_{t+1}) - V^{\pi}(s_{t})))$。当然Advantage函数的形式不只这一种，具体可参考[2]。

2.2 值网络

在上述的Actor-Critic框架中，值网络$V(s, \theta’)$主要用来辅助策略网络的参数$\theta$的更新；同时，值网络同样需要进行训练，值网络的参数更新公式为：$\theta’ \rightarrow \theta’ + \partial(r_{t}-V(s_{t}, \theta’))^{2}/\partial \theta’$

3. A3C算法

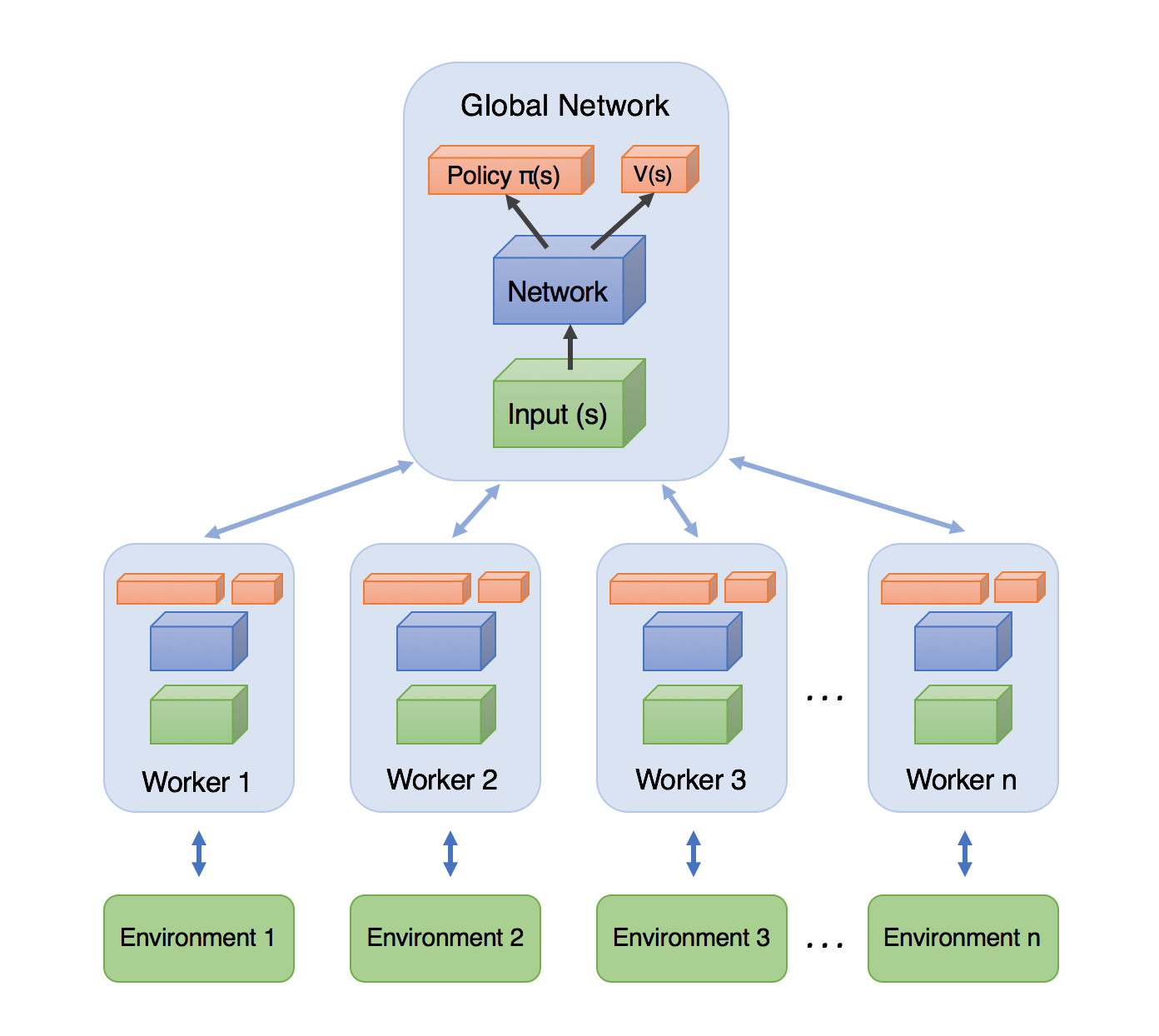
actor-critic-architecture

在上述的算法流程图和示意图[3]中，值得注意的关键点有：

有一个中央控制大脑Global Network，存储着全局参数，负责异步接收各个agent(Worker)的参数梯度来更新全局参数。

各个agent同步中央大脑的参数到自身，再各自进行单独的actor训练。每个agent都先根据策略网络进行训练数据的收集，再累积多个时间步的批量样本来更新策略网络和值网络，这样保证了训练的稳定性。

4. 代码实现[4]

下面以经典Atari游戏中的Breakout为例，基于tensorflow给出整个A3C算法的代码，超参数定义部分省略。

4.1 定义网络结构


class A3CNet(object):
    '''
    策略网络和值网络结合的网络，二者共享网络的卷积层，策略网络负责根据状态选择动作，值网络负责指导策略网络的更新
    '''
    def __init__(self, state_shape, action_dim, scope):

        with tf.variable_scope('%s_placeholder' % scope):
            self.state = tf.placeholder(dtype=tf.float32, shape=[None] + state_shape, name='state')
            self.action = tf.placeholder(dtype=tf.float32, shape=[None, action_dim], name='action')
            self.target_q = tf.placeholder(dtype=tf.float32, shape=[None])

        #shared convnet part
        with tf.variable_scope('%s_shared' % scope):
            self.W1 = tf.get_variable(name='W1', shape=[8, 8, state_shape[-1], 16], initializer=tf.random_uniform_initializer())
            self.b1 = tf.get_variable(name='b1', shape=[16], initializer=tf.constant_initializer(0.0))
            conv1 = tf.nn.relu(tf.nn.bias_add(tf.nn.conv2d(self.state, self.W1, strides=[1, 4, 4, 1], padding='VALID', name='conv1'), self.b1))

            self.W2 = tf.get_variable(name='W2', shape=[4, 4, 16, 32], initializer=tf.random_uniform_initializer())
            self.b2 = tf.get_variable(name='b2', shape=[32], initializer=tf.constant_initializer(0.0))
            conv2 = tf.nn.relu(tf.nn.bias_add(tf.nn.conv2d(conv1, self.W2, strides=[1, 2, 2, 1], padding='VALID', name='conv1'), self.b2))

            flatten1 = tf.reshape(conv2, shape=[-1, 9*9*32], name='flatten1')

            self.W3 = tf.get_variable(name='W3', shape=[9*9*32, 256], initializer=tf.random_uniform_initializer())
            self.b3 = tf.get_variable(name='b3', shape=[256], initializer=tf.constant_initializer(0.0))

            fc1 = tf.nn.relu(tf.matmul(flatten1, self.W3) + self.b3)

        #policy net peculiar
        with tf.variable_scope('%s_policy' % scope):
            self.p_W1 = tf.get_variable(name='p_W1', shape=[256, 256], initializer=tf.random_uniform_initializer())
            self.p_b1 = tf.get_variable(name='p_b1', shape=[256], initializer=tf.constant_initializer(0.0))
            p_fc1 = tf.nn.relu(tf.matmul(fc1, self.p_W1) + self.p_b1)
            self.p_W2 = tf.get_variable(name='p_W2', shape=[256, action_dim], initializer=tf.random_uniform_initializer())
            self.p_b2 = tf.get_variable(name='p_b2', shape=[action_dim], initializer=tf.constant_initializer(0.0))
            p_fc2 = tf.nn.relu(tf.matmul(p_fc1, self.p_W2) + self.p_b2)
            self.policy_out = tf.nn.softmax(p_fc2, name='policy_out')

        #value net peculiar
        with tf.variable_scope('%s_value' % scope):
            self.v_W1 = tf.get_variable(name='v_W1', shape=[256, 256], initializer=tf.random_uniform_initializer())
            self.v_b1 = tf.get_variable(name='v_b1', shape=[256], initializer=tf.constant_initializer(0.0))
            v_fc1 = tf.nn.relu(tf.matmul(fc1, self.v_W1) + self.v_b1)
            self.v_W2 = tf.get_variable(name='v_W2', shape=[256, 1], initializer=tf.random_uniform_initializer())
            self.v_b2 = tf.get_variable(name='v_b2', shape=[1], initializer=tf.constant_initializer(0.0))
            v_fc1 = tf.nn.relu(tf.matmul(v_fc1, self.v_W2) + self.v_b2)
            self.value_out = tf.reshape(v_fc1, [-1], name='value_out')

        #loss value
        with tf.name_scope('%s_loss'%scope, values=[self.policy_out, self.value_out]):
            self.entropy = tf.reduce_sum(self.policy_out * tf.log(self.policy_out + flags.eps))
            self.td_error = self.target_q - self.value_out
            policy_prob = tf.log(tf.reduce_sum(tf.multiply(self.policy_out, self.action), reduction_indices=1))
            self.policy_loss = -tf.reduce_sum(policy_prob * tf.abs(self.td_error)) + self.entropy * flags.entropy_beta
            self.value_loss = tf.reduce_sum(tf.square(self.td_error))

            self.policy_grads = tf.gradients(self.policy_loss, [self.p_W1, self.p_b1, self.p_W2, self.p_b2])
            self.value_grads = tf.gradients(self.value_loss, [self.v_W1, self.v_b1, self.v_W2, self.v_b2])

            self.shared_loss = self.policy_loss + self.value_loss * 0.5
            self.share_grads = tf.gradients(self.shared_loss, [self.W1, self.b1, self.W2, self.b2, self.W3, self.b3])

    def get_policy(self, sess, state):
        return sess.run(self.policy_out, feed_dict={self.state: [state]})[0]

    def get_value(self, sess, state):
        return sess.run(self.value_out, feed_dict={self.state: [state]})[0]

    def get_vars(self):

        return [self.W1, self.b1, self.W2, self.b2, self.W3, self.b3,
                self.p_W1, self.p_b1, self.p_W2, self.p_b2,
                self.v_W1, self.v_b1, self.v_W2, self.v_b2]

上述代码中定义了策略网络和值网络的结构、损失值、梯度值。

4.2 定义各个Agent


class Worker(threading.Thread):
    '''
    负责对中央大脑的值网络和策略网络的参数进行更新和同步的Worker线程
    '''
    def __init__(self, thread_id, master):

        self.thread_id = thread_id
        threading.Thread.__init__(self, name='thread_%d'%thread_id)
        self.env = gym.make('Breakout-v0')
        self.master = master

        self.local_net = A3CNet(state_shape=[84, 84, 4], action_dim=self.env.action_space.n, scope='local_net_%s'%thread_id)
        self.sync = self.sync_network(master.global_net)
        self.accum_grads = self.create_accumulate_gradients()
        self.do_accum_grads_ops = self.do_accmulate_gradients()
        self.reset_accum_grads_ops = self.reset_accumulate_gradients()
        summaries = list()
        summaries.append(tf.summary.scalar('entropy/%d' % thread_id, self.local_net.entropy))
        summaries.append(tf.summary.scalar('policy_loss/%d' % thread_id, self.local_net.policy_loss))
        summaries.append(tf.summary.scalar('value_loss/%d' % thread_id, self.local_net.value_loss))
        summaries.append(tf.summary.scalar('shared_loss/%d' % thread_id, self.local_net.shared_loss))
        self.summary_op = tf.summary.merge(summaries)
        #裁剪各个local net的梯度值
        clip_accum_grads = [tf.clip_by_value(grad, -flags.grad_clip, flags.grad_clip) for grad in self.accum_grads]
        self.apply_gradients = master.optimizer.apply_gradients(
            zip(clip_accum_grads, master.global_net.get_vars()), global_step=master.global_step
        )

    #同步global net的参数到local net
    def sync_network(self, master):
        sync_ops = []
        with tf.name_scope(name='sync_ops_%d'%self.thread_id):
            for (worker_var, master_var) in zip(self.local_net.get_vars(), master.get_vars()):
                ops = tf.assign(worker_var, master_var)
                sync_ops.append(ops)
            return tf.group(*sync_ops, name='sync_group_%d'%self.thread_id)

    #创建各个local net的累积更新梯度值
    def create_accumulate_gradients(self):
        accum_grads = []

        with tf.name_scope(name='create_accum_%d' % self.thread_id, values=[self.local_net]):
            for var in self.local_net.get_vars():
                zero = tf.zeros(var.get_shape().as_list(), dtype=var.dtype)
                accum_grad = tf.Variable(zero, name=var.name.replace(':', '_')+'_accum_grad', trainable=False)
                accum_grads.append(accum_grad)
            return accum_grads

    #累积各个local net的梯度值
    def do_accmulate_gradients(self):
        accum_grad_ops = []

        with tf.name_scope(name='accum_ops_%d'%self.thread_id, values=[]):
            grads = self.local_net.share_grads + self.local_net.policy_grads + self.local_net.value_grads
            for (grad, var, accum_grad) in zip(grads, self.local_net.get_vars(), self.accum_grads):
                accum_ops = tf.assign_add(accum_grad, grad, name=var.name.replace(':', '_')+'accum_grad_ops')
                accum_grad_ops.append(accum_ops)
            return tf.group(*accum_grad_ops, name='accum_group_%d'%self.thread_id)

    #重置各个local net的累积梯度值
    def reset_accumulate_gradients(self):
        reset_grad_ops = []

        with tf.name_scope(name='reset_grad_ops_%d'%self.thread_id, values=[self.local_net]):
            for(var, accum_grad) in zip(self.local_net.get_vars(), self.accum_grads):
                zero = tf.zeros(shape=var.get_shape().as_list(), dtype=var.dtype)
                reset_ops = tf.assign(accum_grad, zero, name=var.name.replace(':', '_')+'reset_grad_ops')
                reset_grad_ops.append(reset_ops)
            return tf.group(*reset_grad_ops, name='accum_group_%d'%self.thread_id)

    #收集训练数据
    def forward_explore(self, train_step):
        terminal = False
        t_start = train_step
        rollout = {
            'state': [],
            'action': [],
            'reward': [],
            'done': []
        }
        state = np.zeros([84, 84, 4], dtype=np.float32)
        while not terminal and (train_step - t_start <= flags.t_max):
            pi_probs = self.local_net.get_policy(self.master.sess, state)
            #基于epsilon-greedy策略的action选择
            if random.random() < 0.8:
                action = np.argmax(pi_probs)
            else:
                action = random.randint(0, self.env.action_space.n - 1)
            observation, reward, terminal = None, None, None
            for _ in xrange(flags.frame_skip):
                observation, reward, terminal, _ = self.env.step(action)
                if terminal:
                    break
            observation = np.resize(observation, new_shape=[84, 84, 1])/256.0
            state = np.append(state[:, :, 1:], observation, axis=2)
            reward = np.clip(reward, -1, 1)
            train_step += 1
            rollout['state'].append(state)
            onehot_action = np.zeros(self.env.action_space.n)
            onehot_action[action] = 1
            rollout['action'].append(onehot_action)
            rollout['reward'].append(reward)
            rollout['done'].append(terminal)
        return train_step, rollout

    def run(self):
        sess = self.master.sess
        self.env.reset()
        loop = 0
        while flags.train_step <= flags.t_train:
            train_step = 0
            loop += 1
            sess.run(self.reset_accum_grads_ops)
            sess.run(self.sync)
            train_step, rollout = self.forward_explore(train_step)
            if rollout['done'][-1]:
                rollout['reward'][-1] = 0
                self.env.reset()
            else:
                rollout['reward'][-1] = self.local_net.get_value(sess, rollout['state'][-1])
            rollout['return'] = scipy.signal.lfilter([1], [1, flags.gamma], rollout['reward'][::-1], axis=0)[::-1]
            fetches = [self.do_accum_grads_ops, self.master.global_step]
            lc_net = self.local_net
            if loop % 10 == 0:
                fetches.append(self.summary_op)
            result = sess.run(fetches, feed_dict={
                lc_net.state: rollout['state'],
                lc_net.action: rollout['action'],
                lc_net.target_q: rollout['return']
            })
            if loop % 10 == 0:
                global_step, summary_str = result[1:3]
                self.master.summary_writer.add_summary(summary_str, global_step=global_step)
                self.master.global_step_val = int(global_step)
            sess.run(self.apply_gradients)
            flags.train_step += train_step
            if loop % 10 == 0 and self.thread_id == 0:
                print('thread_id=%d, loop=%d, train_step=%d' % (self.thread_id, loop, flags.train_step))
                self.test()
            if loop % 1000 == 0 and self.thread_id == 0:
                checkpoint_filename = self.master.saver.save(sess, flags.train_dir + '/' + 'a3c_model', global_step=self.master.global_step_eval)

    def test(self, episode=10, max_step=1e3):
        rewards = []
        start_time = time.time()
        while episode > 0:
            terminal = False
            self.env.reset()
            episode_reward = 0
            test_step = 0
            state = np.zeros([84, 84, 4], dtype=np.float32)
            while not terminal and test_step < max_step:
                pi_probs = self.local_net.get_policy(self.master.sess, state)
                action = np.argmax(pi_probs)
                observation, reward = None, None
                for _ in xrange(flags.frame_skip):
                    observation, reward, terminal, _ = self.env.step(action)
                    if terminal:
                        break
                observation = np.resize(observation, new_shape=[84, 84, 1])/256.0
                state = np.append(state[:, :, 1:], observation, axis=2)
                test_step += 1
                reward = np.clip(reward, -1, 1)
                episode_reward += reward
            rewards.append(episode_reward)
            episode -= 1
        elapsed_time = int(time.time() - start_time)
        print('train-step = %d, avg_reward = %.2f, time=%d(s)' % (flags.train_step, reduce(lambda x, y: x+y, rewards), elapsed_time))

上述代码定义了每个Agent同步来自全局大脑的参数、梯度累积、数据收集、独自训练、效果测试的过程。

4.3 执行实际的训练过程


class A3CAtari(object):
    '''
    定义中央大脑、执行整个网络的训练
    '''
    def __init__(self):
        self.env = gym.make('Breakout-v0')
        self.graph = tf.get_default_graph()
        self.global_net = A3CNet(state_shape=[84, 84, 4], action_dim=self.env.action_space.n, scope='global_net')
        self.optimizer = tf.train.AdamOptimizer(flags.learning_rate, name='global_optimizer')
        self.global_step = tf.get_variable('global_step', [], initializer= tf.constant_initializer(0), trainable=False)
        self.summary_writer = tf.summary.FileWriter(logdir=flags.train_dir, graph=self.graph)
        self.jobs = []
        for thread_id in xrange(flags.jobs):
            self.jobs.append(Worker(thread_id, self))
        self.sess = tf.Session(config=tf.ConfigProto(log_device_placement=False, allow_soft_placement=True))
        self.sess.run(tf.global_variables_initializer())
        self.global_step_eval = 0
        self.saver = tf.train.Saver(var_list=self.global_net.get_vars(), max_to_keep=3)
        #self.saver.restore(self.sess, flags.train_dir)

    def train(self):
        flags.train_step = 0
        signal.signal(signal.SIGINT, signal_handler)
        for job in self.jobs:
            job.start()
        for job in self.jobs:
            job.join()

def signal_handler():
    sys.exit(0)

def main(_):
    if not os.path.isdir(flags.train_dir):
        os.mkdir(flags.train_dir)
    for f in os.listdir(flags.train_dir):
        if re.search('.*tfevents.*', f):
            os.remove(os.path.join(flags.train_dir, f))
    model = A3CAtari()
    model.train()

if __name__ == '__main__':
    tf.app.run()

上述代码定义了中央大脑和各个训练Worker，启动整个网络的训练。

参考资料

[1] Asynchronous Methods for Deep Reinforcement Learning
[2] High-Dimensional Continuous Control Using Generalized Advantage Estimation
[3] Simple Reinforcement Learning with Tensorflow Part 8: Asynchronous Actor-Critic Agents (A3C)
[4] Github上A3C算法的实现